I’m assuming y’all know about means. In my home school district mean, median, and mode were all taught in third or fourth grade and referenced occasionally in math classes subsequently. But I’m guessing you don’t know about types of means.

See, the mean we’re familiar with is more properly called the “arithmetic mean,” so called because it uses simple arithmetic. But there are others that show up in statistics and other scientific applications. The most common are the geometric mean, the harmonic mean, and the quadratic mean (also often called the root mean square). And all of these are based on the generalized f-mean.

A note before we start: in all of these examples, I’m going to use the data set {7, 9, 29, 40, 42, 42, 65,
70, 87, 89}, which has an arithmetic mean of 48.

Harmonic mean

The harmonic mean is actually pretty simple: it’s the inverse of the average of the inverses of your data. In mathematical notation, that’s

H=(\frac{\sum\limits_{i=1}^{n}\frac{1}{x_{i}}}{n})^{-1}=n\cdot(\sum\limits_{i=1}^{n}\frac{1}{x_{i}})^{-1}

So let’s do an example. The first thing you do is find the inverse (\frac{1}{x}) of each item; in decimal that’s {0.011, 0.011, 0.014, 0.015, 0.024, 0.024, 0.025, 0.034, 0.111, 0.143}. Now we find the mean (\bar{x}) of these inverses. The sum of these is 0.412, and divided by 10 gives us \bar{x}=0.0412. Now all we have to do is find the inverse \frac{1}{\bar{x}}, which is 24.186*.

Quadratic mean

The quadratic mean (or root mean square) is likewise fairly simple; the only difference is that you square rather than inversing the data, and square root the resulting average. So in mathematical notation, that’s

x_{RMS} = \sqrt{\frac{\sum\limits_{i=1}^{n}x_{i}^{2}}{n}}

Example time again. First we square each of the items, which gives us {49, 81, 481, 1600, 1764, 1764, 4225, 4900, 7569, 7921}. Summing gives us 30354, and dividing by 10 gives us \bar{x}=3035.4. Now we find the square root of that to give us 55.42.

Geometric mean

The geometric mean is somewhat more difficult to calculate, but it’s probably my favorite. In middle school I independently “invented” it while I was bored in math class, but pretty quickly gave it up because it turned out to be too unwieldy to calculate.

Now, if you’re familiar with arithmetic, quadratic, and geometric growth (which you should be) you might be able to guess what the geometric mean is. If not, here’s a hint:

Arithmetic, quadratic, and exponential growth.

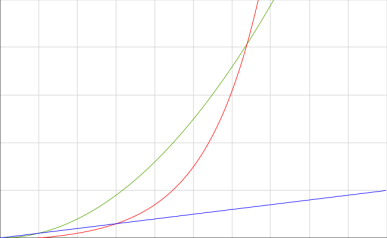
This graph shows arithmetic growth (y = x) in blue, quadratic growth (y = x^2) in green, and geometric growth (y = 2^x) in red.

If you guessed that calculating the geometric mean involves multiplying your data together, you’re correct and win a prize**!

The mathematical notation for the geometric mean involves a symbol there’s a good chance you haven’t seen (I know I hadn’t until I learned about geometric means): \prod\limits_{i=1}^{\infty}. That’s the product sign, and is essentially the equivalent of \sum\limits_{i=1}^{\infty}, except instead of adding the items together, you multiply them. So, the notation is:

G=\sqrt[n]{\prod\limits_{i=1}^{n}x_i}=(\prod\limits_{i=1}^{n}x_i)^{\frac{1}{n}}

So, we could calculate that as it is, by finding the product of our ten numbers (4,541,693,011,128,000, over 4½ quadrillion) and then the 10th root of that (36.789). Which is fine. But if we had any more numbers, my calculator would overflow, and sometimes you need to calculate the geometric mean of hundreds of numbers. To avoid having to use a computer with a googol bytes of memory, we take advantage of logarithms.

If you took pre-calculus with Mr. Kawamura, you might remember—will remember, considering how much he drilled it into our heads—that \log (x\cdot y)=\log x + \log y. What this means is that you can turn a product into a sum, which is a lot easier to deal with. So what we do is take the natural log*** of both sides of the equation, giving us

\ln G= \frac{\sum\limits_{i=1}^{n}\ln x_i}{n}

Which is a hell of a lot easier to calculate.

So let’s go back to our example data set. The natural logarithms of the items are {1.946, 2.197, 3.367, 3.689, 3.738, 3.738, 4.174, 4.248, 4.466, 4.489}. The sum of those is 36.052, which divided by 10 gives us \ln G=3.6052. But that’s only the natural log of G, so now we have to reverse the logarithm by finding e^{3.6052}, which turns out to be 36.789.

By now it should be obvious that the means for this dataset are not the same. To review, we’ve got:

Mean Type Mean
Arithmetic 48
Harmonic 24.186
Quadratic 55.42
Geometric 36.789

In other words, H < G < \bar{x} < x_{RMS}. And this is always true. (Unless all of your items are equal, in which case you wouldn’t bother calculating a mean, now would you?)

Generic f-mean

Now you may be seeing a pattern here. All of these different means follow basically the same form. This form is called the generic f-mean. It can be described thusly:

\bar{x}(f) = f^{-1}(\frac{\sum\limits_{i=1}{n}f(x_i)}{n})

The only real restriction on this is that f be an invertible function. So you could go wild with this. You could use f(x)=\sin (x) (for -½π < x < ½π). You could use f(x) = \frac{xe^{-x^2}}{x^2+x}. Hell, you could use f(x) = \int_0^1 3^x.

I’m not really sure what to write in conclusion, other than “means are cool!” so I’ll just leave it here. In a while I’ll come back to this topic. Coming up Wednesday, though, is a post on sample sizes and why (some) psychologists are stupid.

*Incidentally, were you to do this by hand and round as I did to the thousandth place, the math doesn’t add up exactly because of rounding errors.

**1.0 cookies****, redeemable by mail!

***You can actually use any base you want for the logarithm, since we’ll be reversing it. I just use ln since I’m a biology geek and e turns up a lot more than 10.

****With a 95% margin of error of 2.0 cookies.

Resources

Random.org Where I got the example dataset.

Mean at Wikipedia

Statistics Calculators Includes calculators for all of the means (other than the generic f-mean) that I discussed here.

\LaTeX on WordPress How I did all the equations.

Basics, Summary Statistics

June 25, 2012

Leave a comment